简介 (About the summer school)

This summer school is hosted by the Kavli Institute for Theoretical Sciences (KITS) of University of Chinese Academy of Sciences. The summer school aims at exposing students and postdocs to the frontiers in theoretical high energy physics and introducing to them the basic research techniques. The area is broadly quantum field theory and string theory. The topics include: Conformal field theory, scattering amplitudes, large charge expansion, integrability, QCD strings etc. The school consists of regular lectures and a poster session for interested students and postdocs.

本次暑期学校由中国科学院大学卡弗里理论科学研究所主办。目的是帮助学生与博士后接触到现代高能理论物理的研究前沿，并学习这些领域的基本的研究技巧。 本次的暑期学校的课程内容主要涉及量子场论与弦理论。具体包括的主题有：共形场论、散射振幅、大荷展开、可积性以及QCD弦论等。 本次暑期学校包括一些常规的系列讲座以及一次由学生与博士后参加的海报展示。

报告人 (Speakers)

• Patrick Dorey (Durham University)
Title: Exact S-matrices in 1+1 dimensions
Abstract: These lectures will discuss the basics of the theory of exact (relativistic) S-matrices in 1+1 dimensions. Topics to be covered include conservation laws and factorability, properties of the 2-particle S-matrix, and pole structure and the Coleman-Thun mechanism, using the sine-Gordon model, perturbed minimal models, and the affine Toda field theories as the main examples. If there’s time at the end I may also mention the TBA technique, and give a quick sketch of the simplest examples of the ODE/IM correspondence.
Reading material: Exact S-matrices Lectures on Non Perturbative Field Theory and Quantum Impurity Problems Lectures on Non Perturbative Field Theory and Quantum Impurity Problems: Part II An Integrability Primer for the Gauge-Gravity Correspondence: an Introduction G. Mussardo, Off-critical statistical models: Factorized scattering theories and bootstrap program, Phys. Rep. 216 (1992) 215 — 379

• Vasco Goncalves (University of Porto)
Title: Analytical conformal bootstrap
Abstract: This lecture will provide an overview of the analytical conformal bootstrap program for studying conformal field theories. I will outline the core concepts of conformal symmetry, operator product expansions, and crossing symmetry that underlie the bootstrap approach. I will review several methods that have been used over the years and when they are applicable. I will also make connections with several open problems.
Reading material: TASI Lectures on the Conformal Bootstrap, EPFL Lectures on Conformal Field Theory in D ≥ 3 Dimensions

• Jie Gu (Southeast University)
Title: Resurgence Theory and Applications in Quantum Physics
Abstract: In the course of these lectures, I will explain the basic ideas behind the resurgence theory, a powerful mathematical framework to study a particular class of divergent power series, the 1-Gevrey series, to which perturbative series in physics usually belong, as well as some of its applications in physics. An important message from the resurgence theory is that a perturbative series and its non-perturbative corrections are intimately related and the latter can be extracted from the former. I also discuss the application of the resurgence theory in both quantum mechanics (QM) and supersymmetric quantum field theories (SQFT). In QM, the exact WKB method based on resurgence techniques allows derivation of exact quantisation conditions of energy spectrum and full energy trans-series. In SQFT, non-perturbative corrections to free energy and Wilson loops can be uncovered by resurgence considerations. These two themes in QM and SQFT are then surprisingly connected through the BPS invariants of the SQFT.
Reading material:
Resurgence: Lectures on non-perturbative effects in large N gauge theories, matrix models and strings, A Primer on Resurgent Transseries and Their Asymptotics, Introduction to 1-summability and resurgence
Resurgence in SQFT: Introduction to Seiberg-Witten Theory and its Stringy Origin, Wall-crossing, Hitchin Systems, and the WKB Approximation, Non-perturbative approaches to the quantum Seiberg-Witten curve, On the resurgent structure of quantum periods, Relations between Stokes constants of unrefined and Nekrasov-Shatashvili topological strings, Resurgent Structure of the Topological String and the First Painlevé Equation, Resurgence of refined topological strings and dual partition functions
Exact WKB: Andre Voros, The return of the quartic oscillator. The complex WKB method; Marcos Marino, Advanced Topics in Quantum Mechanics

• Song He (Institute of Theoretical Physics, CAS)
Title: Title: From combinatorics to real-world scattering
Abstract: I will give an introduction to the new subject of combinatorial geometries for particle (and string) scattering amplitudes, from the simplest colored scalar theory to the real-world scattering of pions, gluons etc.
Reading material: Scattering Forms and the Positive Geometry of Kinematics, Color and the Worldsheet, Causal Diamonds, Cluster Polytopes and Scattering Amplitudes, Stringy Canonical Forms, Binary Geometries, Generalized Particles and Strings, and Cluster Algebras, All Loop Scattering as a Counting Problem, All Loop Scattering For All Multiplicity, Hidden zeros for particle/string amplitudes and the unity of colored scalars, pions and gluons, Scalar-Scaffolded Gluons and the Combinatorial Origins of Yang-Mills Theory, NLSM $\subset \text{Tr}(\varphi^3)$,

• Florian Loebbert (University of Bonn)
Title: Integrability for Feynman Integrals
Abstract: Feynman integrals are crucial ingredients for calculations within quantum field theory and key to phenomenological predictions. A new tool for their investigation comes with the recent discovery of integrable structures for large families of Feynman graphs and the associated symmetry constraints. These constraints can be formulated in terms of the conformal Yangian and result in differential equations for the considered integrals. Here we give a pedagogical introduction to the Yangian symmetry of Feynman integrals and associated bootstrap approaches. We review connections to AdS/CFT integrability via the so-called fishnet theories and comment on the recent relation between Yangian symmetry and Calabi-Yau geometry for integrals in two spacetime dimensions.
Reading material: Integrability for Feynman Integrals, Complete list of references.

• Carlos Mafra (University of Southampton)
Title: Tree-level amplitudes from the pure spinor superstring
Abstract: In these lectures I will review the pure spinor techniques used in the calculation of the massless n-point string tree-level amplitudes, and related topics.
Reading material: The main reference is the review Tree-level amplitudes from the pure spinor superstring

• Domenico Orlando (INFN, Turin)
Title: The large-charge expansion in CFT
Abstract: We discuss the general construction of the large charge using the examples of the O(2) and O(2N) model and we reproduce the results from the EFT using as microscopic model the vector model at large N. In this case we can also use resurgence to compute non-perturbative exponentially-suppressed terms.
Reading material: Selected Topics in the Large Quantum Number Expansion, Resurgence of the large-charge expansion

• Deliang Zhong (Imperial College, London)
Title: Introduction to AdS/CFT integrability
Abstract: $\mathcal{N}=4$ spin chains, Integrable techniques to solve the spin chain energy, Integrable $\sigma$-model, Bootstrapping the worldsheet S-matrix
Reading material:
Lecture I: $\cal{N}=4$ SYM Spin Chains
1.1 A brief introduction to AdS/CFT
1.2 $\cal{N}=4$ SYM action from dimensional reduction
1.3 Double-line notation and large N counting
1.4 Radial quantisation
1.5 1-loop dilatation operator in the $\text{SO}(6)$ sector
Lecture II: Bethe Ansatz
2.1 SU(2) sector and the Heisenberg model
2.2 Coordinate Bethe Ansatz
2.3 Bethe Ansatz equation in the $\text{SO}(6)$ sector
2.4 Nested Bethe Ansatz
References: Review of AdS/CFT Integrability, Chapter I.1: Spin Chains in $\cal{N}=4$ Super Yang-Mills, Factorized S-matrix and the Bethe ansatz for simple lie groups
Lecture III: Bootstrapping the $\cal{N}=4$ S-matrix
3.1 Induced representation & little group
3.2 Asymptotic description, central extension and the large gauge transformations
3.3 Finite-size corrections: idea of thermodynamic Bethe Ansatz
References: Review of AdS/CFT Integrability, Chapter III.2: Exact world-sheet S-matrix, Section 3.2 of Lectures on Three-point Functions in $\cal{N}=4$ Supersymmetric Yang-Mills Theory, The $su(2|3)$ Dynamic Spin Chain, TThe Analytic Bethe Ansatz for a Chain with Centrally Extended $su(2|2)$ Symmetry
Lecture IV: Integrability Approach to 3pt Functions
4.1 3pt function of BPS operators
4.2 The idea of “tayloring”
4.3 Induced representation & little group for 3pt
4.4 Asymptotic Hexagon form factor
4.5 “Hexagonization” approach to higher point functions
Reference: Sections 2 and 3.3 of Lectures on Three-point Functions in $\cal{N}=4$ Supersymmetric Yang-Mills Theory
Things skipped in the lecture:
5.1 QSC Formalism
Reference: Introduction to the Spectrum of $\cal{N}=4$ SYM and the Quantum Spectral Curve




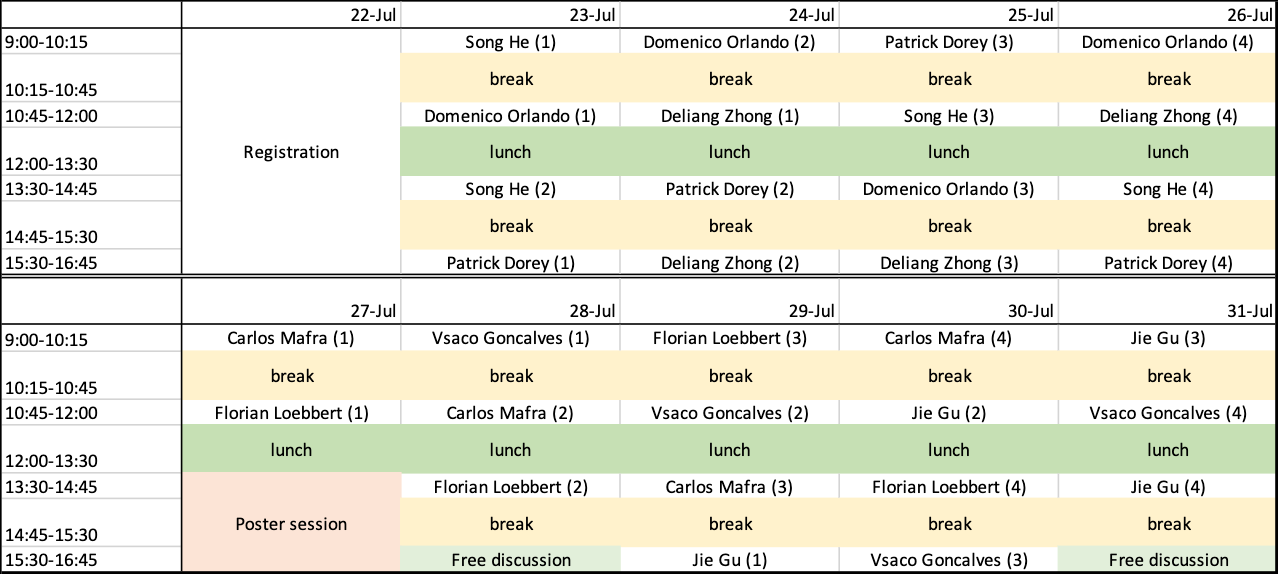
会议日程 (Schedule)

申请 (Applying to the summer school)

The summer school is open for applications to advanced graduate students (must have taken courses in QFT and have some familiarity with CFTs and string theory) and postdocs. Applications should be submitted via the QR code on the poster (or click here) and should include the following materials:
1. A brief CV (not required for faculty),
2. A publication list of 5 representative works (if any),
3. A recommendation letter from your advisor (not necessary for postdocs),
4. A one-page description of your poster presentation (if you wish to present).
These materials should be combined into a single pdf file in this order. The deadline of applications is June the 15th. Successful applicants will be informed in late June.

本次暑期学校面向的是高年级研究生（必须修过量子场论并对共形场论与弦论有一定的掌握）与博士后。申请需通过海报上的二维码（或者点击 这里）提交且应包含以下材料
1. 个人简历 (仅学生和博士后要求)，
2. 不超过5篇代表作列表（若有），
3. 导师签名的推荐信一封（博士后不要求），
4. 一页以内关于你想在海报中展示的工作内容（如果希望参与）。
请将以上内容按顺序合并成一个pdf文件。申请的截止日期为2024年6月15日。成功通过的申请者将于六月底通过邮件通知。


Financial support: The applicants are encouraged to have their own sources of funding to cover their expenses during the school. However, students in financial difficulties may apply for support by indicating so in the application form. The amount of funding is limited and can only cover a small number of students.

资助：一般情况下申请者须自己解决差旅与住宿的费用。对于有特别困难的学生，有一定的资助名额可以申请。

会议组织 (Summer school organization)

Organizers:

• Cheng Peng
• Konstantinos Rigatos
• Huajia Wang
• Zhefei Yu
• Fu-Chun Zhang
• Xinan Zhou

联系方式 (Contact us)

Any questions about the school should be sent to the main organizer: xinan.zhou at ucas.ac.cn .
任何关于暑期学校的问题请发送至组织者的邮箱：xinan.zhou at ucas.ac.cn